A function is a rule of correspondance by which when anything is given (as argument) another thing (the value of the function for that argument) may be obtained. This definition is found on page 1 of The Calculi of Lambda-Conversion by Alonzo Church, Princeton University Press, copyright 1941. This can be written \( f(x) = y \).
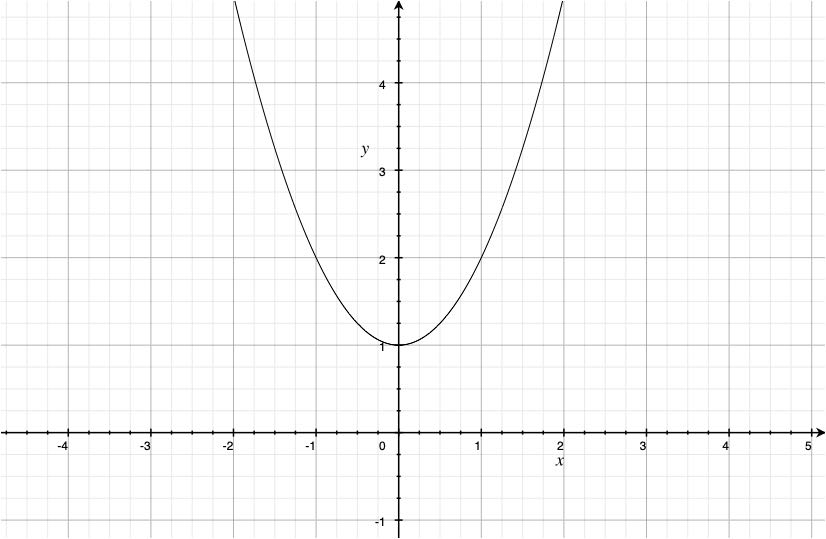
Graphing gives a picture of a function and can be helpful for understanding
the function. The graph of the function \( y = x^2 + 1 \) is shown below.

If the function graphed above, both the arguments and values are numbers. The general notion of a function does not require this. The arguments and values can be quite general. We will see the case where the arguments and values are themselves functions.
A set is a collection of objects. Which doesn't help much since a collection is a set of things. Hopefully this notion of a set is intuitive. Given an object \(u\) and a set \(S\), then the expression \(u \in S\) says that \(u\) is in the set \(S\). That \(u\) is not is \(S\) is written \( u \not\in S \). Alternatively, the expression \(u \in S\) can be treated as a sentence that is either True or False depending on whether \(u\) is in \(S\).
If \(S\) and \(T\) are sets, then \(S = T\) if, and only if, they have the same elements. The union of \(S\) and \(T\), denoted \(S \cup T\) is the set that contains all the elements that are in \(S\) or in \(T\) or both. The intersection of \(S\) and \(T\), written \(S \cap T\) consists of all the elements that are in both \(S\) and \(T\). If every element of \(S\) is in \(T\) then \(S\) is a subset of \(T\), and this is indicated by \(S \subset T\) or equivalently \(T \supset S\). \(S\) and \(T\) are equal if, and only if, they have the same elements. Equality can be established by showing both \(S \subset T\) and \(T \subset S\).
If we are working with subsets of some big set \( \mathbf{B} \) then we define the complement of a set \(S \subset \mathbf{B} \) denoted \(S'\) is the set \( \{ b \in \mathbf{B} | b \not\in S \} \). The vertical bar "|" is read "such that".
The domain of a function is the set of values for which it is defined. The function \(f: x \rightarrow x^2 \) is defined for all real real numbers. The function \(g: y \rightarrow \sqrt{y} \) is defined for all \( y \geq 0 \).
The range of a function is the set where the values lie. The range of the functions \(f\) and \(g\) is the set of all real numbers.
A convenient notation to specify the domain and range of a function is \( f:D \rightarrow R \) says that \(f\) is a function with domain \(D\) and range \(R\).
The image of a function is the set of values that the function takes on, and is a subset of the range. Both \(f\) and \(g\) have image the set of non-negative real numbers.
A function \(h\) is 1-1 (one to one) if \(x_1 \not= x_2\) then \(h(x_1) \not= h(x_2)\). \(h\) is onto if for any \(y\) in the range of \(h\) there is an \(x\) in the domain of \(h\) with \(h(x) = y\).
The function \(f\) is not 1-1 since \(f(-2) = f(2) = 4\). By restricting the domain of \(f\) to just the non-negative reals the resulting function will be 1-1.
Two functions \(h_1\) and \(h_2\) are equal if they have the same domain and range, and for all \(x\) in the common domain, \( h_1(x) = h_2(x) \). It may be the case that \(h_1\) and \(h_2\) are specified by different formulas or different computation rules, but nevertheless they always have the same value. If it's important to distinguish this case, we say that \(h_1 = h_2\) in extension but not in intention.
An extension to the notion of a function is to allow multiple arguments. For example define \(add(x,y) = x + y\).
An order pair of numbers has a first number and a second number and is written using parentheses as \( (a, b) \). The ordered pairs \( p = (a, b) \) and \( q = (c, d) \) are equal if and only if \( a = c \) and \( b = d \). This extends to ordered n-tuples.
An ordered pair of real numbers can be defined as a function from the set {1, 2} to the real numbers. If f is such a function, then the first coordinate is f(1) and the second is f(2). The equality of pairs is the same as the equality of functions. This can be extended to ordered n-tuples by changing the domain to \( \lbrace 1, 2, \ldots , n \rbrace \).
From functions \(f\) and \(g\) we can create three new functions:
For functions \(f\) and \(g\) with domain and range both subsets of the real line:
If \(f\) is a function, the inverse, written \(f ^ {-1} \), which is easy to confuse with \( \frac{1}{f} \), is defined by \(f ^ {-1}(A) \) is the set \( \lbrace x | f(x) \in A \rbrace \) for sets \(A\). For a single item \(y\), \( f ^ {-1} (y) \) is understood to mean \( \lbrace x | f(x) = y \rbrace \).
What conditions must be placed on a function \(f:D \rightarrow R\) so that \(f^{-1} : R \rightarrow D\) is a function? Hint: a function gives one value in its range for each argument from its domain.
If \(A\) and \(B\) are subsets of \(R\), then prove or give a counter example for the following:
Return to the table of contents